View 22 Partial Derivatives, Tangent Planes, Linear Approximationpdf from MATH 53 at University of California, Berkeley PoyffffIfn n x and y B Partialderivative nfwrtX É xy s fx xAnswer to Find the partial derivative for x f(x,y)=\frac{1}{\sqrt{x^{2}y^{2}}} By signing up, you'll get thousands of stepbystep solutions to@f @x = 2xe2x3 e 2x y;
Http Www Maths Gla Ac Uk Cc 2x 05 2xnotes 2x Chap1 Pdf
Partial derivative of log(x^2+y^2)
Partial derivative of log(x^2+y^2)- I have a function g as a function of x;Then I'll find the second derivative of F with respect to X And with respect to X Again, to do this, I will in the partial derivative of F with respect to X, hold Y constant and differentiate with respect to X Again, so I get 12 X squared y squared minus six X Y Yeah I'll also find the second partial derivative of F With respect to X



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf
Section73 Partial Differentiation ¶ 🔗 The derivative of a function of a single variable tells us how quickly the value of the function changes as the value of the independent variable changes Intuitively, it tells us how "steep" the graph of the function is We might wonder if there is a similar idea for graphs of functions of twoFind partial derivative of the following 1) f(x, y) = 3x cos(x) cos(y) df'/dx=?@f @y = 4 (b) f(x;y) = xy3 x 2y 2;
F' x = y 3 cos (x) 2x tan (y) Likewise with respect to y we turn the "x" into a "k" f (x, y) = y 3 sin ( k) k 2 tan (y) f' y = 3y 2 sin (k) k 2 sec 2 (y) f' y = 3y 2 sin (x) x 2 sec 2 (y) But only do this if you have trouble remembering, as it is a little extra work $$\frac{\partial}{\partial x} \ln(x^2y^2)$$ now if this was just $\frac{d}{dx}\ln(x^2)$ we would get $\frac{2x}{x^2}$ So I feel we would get$$\frac{\partial}{\partial x} \ln(x^2y^2)=\frac{2x}{x^2y^2}$$Please Subscribe here, thank you!!!
The partial derivative of a function of multiple variables is the instantaneous rate of change or slope of the function in one of the coordinate directions Computationally, partial differentiation works the same way as singlevariable differentiation with all other variables treated as constant The partial derivative of a function f (x, y) f(x,y) f (x, y) in the x x xdirection can be//googl/JQ8NysPartial Derivative of f(x, y) = xy/(x^2 y^2) with Quotient Rule@f @x = 3;



Http Www Maths Gla Ac Uk Cc 2x 05 2xnotes 2x Chap1 Pdf
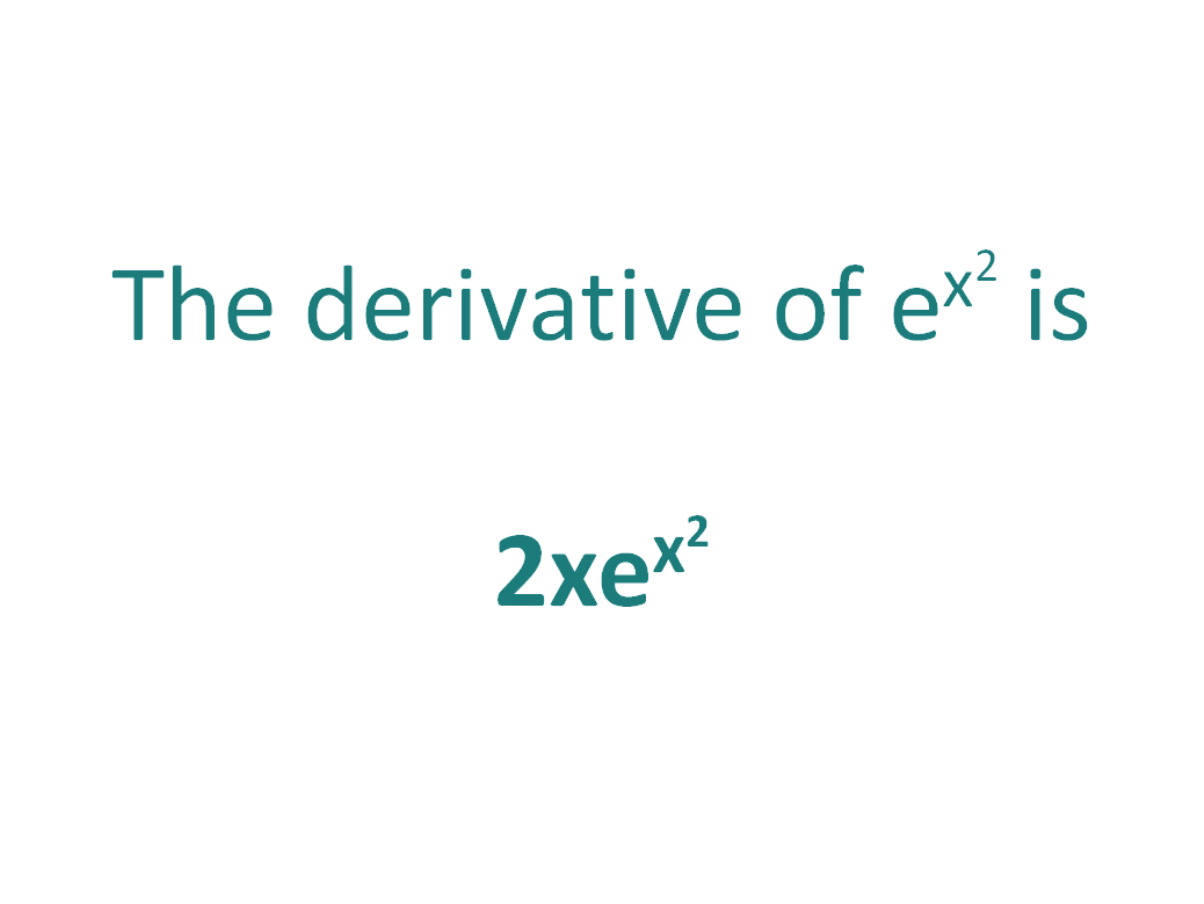



The Derivative Of E X 2 Derivativeit
Find stepbystep solutions and your answer to the following textbook question Find the indicated partial derivative(s) f(x,y)=sin(2x5y);Differentiate (x^2 y)/(y^2 x) wrt x;In this section the subscript notation f y denotes a function contingent on a fixed value of y, and not a partial derivative Once a value of y is chosen, say a, then f(x,y) determines a function f a which traces a curve x 2 ax a 2 on the plane =




Calculus 3 Partial Derivative 14 Of 30 Find More Partial Derivatives Example 2 Of 2 Youtube




Compute The Partial Derivatives Of F X Y Log U Chegg Com
2)f(x, y) = 3(x 2 y 2) log(x 2 y 2), (x, y) ?Find fxx, fyy given that f (x , y) = sin (x y) Solution f xx may be calculated as follows fxx = ∂2f / ∂x2 = ∂ (∂f / ∂x) / ∂x = ∂ (∂ sin (x y) / ∂x) / ∂x = ∂ (y cos (x y) ) / ∂x = y2 sin (x y) ) f yy can be calculated as follows fyy = ∂2f / ∂y2 = ∂ (∂f / ∂y) / ∂y@f @y = (x
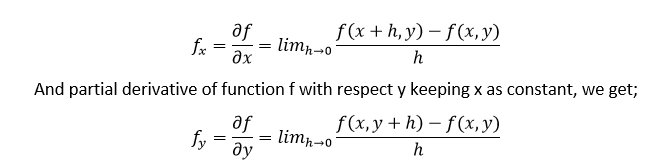



Partial Derivative Definition Formulas And Examples Partial Differentiation




Find Partial Differential F Partial Differential X Chegg Com
To find d/dx(sqrt(x^2y^2)), as part of an implicit differentiation problem, use the chain rule d/dx(sqrtx) = 1/(2sqrtx), so d/dx(sqrtu) = 1/(2sqrtu) (du)/dx d/dx(sqrt(x^2y^2)) = 1/(2sqrt(x^2y^2)) * d/dx(x^2y^2) = 1/(2sqrt(x^2y^2))(2x2y dy/dx) =1/(2sqrt(x^2y^2))2x 1/(2sqrt(x^2y^2))2y dy/dx =x/sqrt(x^2y^2) y/sqrt(x^2y^2) dy/dx In order to solve for dy/dx you will, of course, need the rest of the derivativeEnter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask for a derivative derivative of arcsin;But the y2 term is an additive constant, hence disappears z = 3x 2y2 y ∂ ∂ Note that the 5x4 disappears because it is an additive constant;




For Any Function F X Y The First Partial Derivatives Are Represented By F F Fx And Fy X Y For Example If F X Y Log X Sin Ppt Video




21 Partial Derivatives Problem 4 Most Important Problem Partial Differentiation Youtube
Second derivative of sin^2;The partial derivative with respect to x is computed by keeping y constant;Solutions to Examples on Partial Derivatives 1 (a) f(x;y) = 3x 4y;
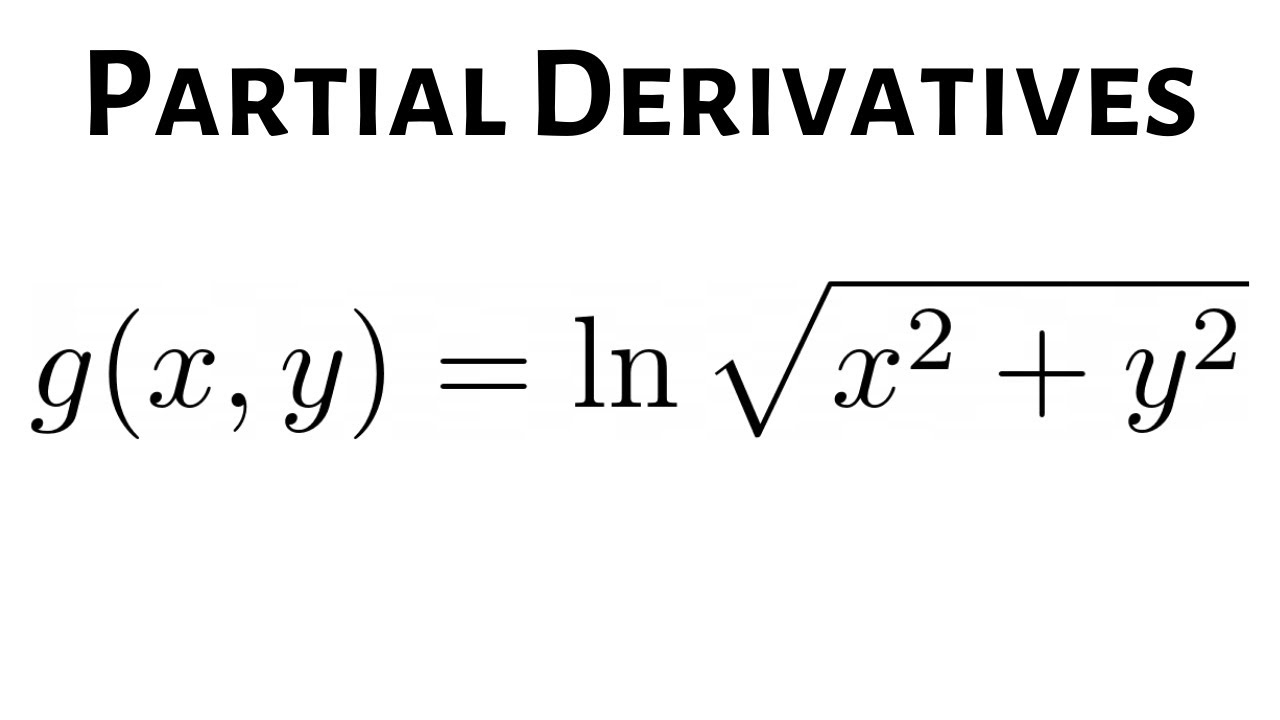



Larson Calculus 13 3 28 First Partial Derivatives Of G X Y Ln Sqrt X 2 Y 2 Youtube
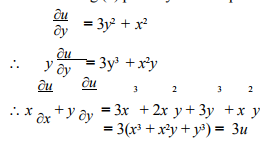



Partial Derivatives Differentiation Business Mathematics Statistics B Com Notes Edurev
מחשבונים לאלגברה, חשבון אינפיטיסימלי, גאומטריה, סטטיסטיקה, וכימיה כולל הדרךDerivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Functions Line Equations Functions Arithmetic & Comp ConicConsequently, the derivative of the logarithmic function has the form (logax)′ = 1 x logae By the changeofbase formula for logarithms, we have logae = lne lna = 1 lna Thus, y′(x) = (logax)′ = 1 xlna If a = e, we obtain the natural logarithm the derivative of which is expressed by the formula (lnx)′ = 1 x




Derivative Of Log Confusion Mathematics Stack Exchange



14 3 Partial Differentiation
So you get \frac{\partial f}{\partial x}=y\log(1\sqrt{x^22y^2})xy\frac{\dfrac{x}{\sqrtDerivative of arctanx at x=0;U}{\partial y \partial x} $




Natural Logarithm Wikipedia




Finding The Derivative Of Log X Video Lesson Transcript Study Com
= sec 2 (xy) y cos x = y sec 2 (xy) cos x Now, Derivative of a function with respect to y So, x is constant fy = ∂ f ∂ y \frac{\partial f}{\partial y} ∂ y ∂ f = ∂ ∂ y \frac{\partial}{\partial y} ∂ y ∂ tan (x y) sin x \tan (xy) \sin x tan (x y) sin x@f @y = 3xe (e) f(x;y) = x y x y @f @x = x y (x y) (x y)2 = 2y (x y)2;Take log to get log u = x log y 1/u ∂u/∂x= log y => ∂u/∂x = ulogy =(y^x)*log y Similarly 1/u∂u/∂y = x/y => ∂u/∂y = ux/y = xy^(x1)




Symmetry Of Second Partial Derivatives Video Khan Academy




Implicit And Logarithmic Differentiation
Derivative of x/(x^2y^2) by x = (y^2x^2)/(y^42*x^2*y^2x^4) Show a step by step solution;By holding y fixed and differentiating with respect to x\text {,} we obtain the firstorder partial derivative of f with respect to x Denoting this partial derivative as f_x\text {,} we have seen that provided this limit exists In the same way, we may obtain a trace by setting, say, x=150 as shown in Figure 102I want to take derivative of g with respect to ln x, ie dg/d ln x where g= ax^2/(1ax^2/r^2) Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their




If U Log X 2 Y 2 Z 2 Then X 2u Y Z Y 2u Z X Z 2u X Y




Asgscv Partial Differential Equation Rates
Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Functions Line Equations Functions Arithmetic & Comp Conic Sections Transformation@f @y = 3xy 2xy (c) f(x;y) = x 3y ex;Question Partial Derivatives Find ∂f ∂x (partial derivative of x) ∂f ∂y (partial derivative of y) for the following f(x, y) = 5(x2 y2) log(x2 y2), (x, y) ≠ (0, 0) This problem has been solved!
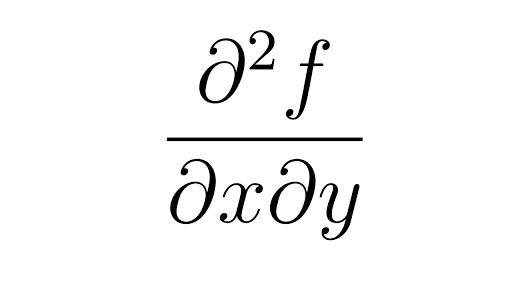



Second Partial Derivatives Article Khan Academy




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange
Right We want to find the first partial derivative of a function F of X Y is equal to X squared hems E Raised to the power of wide square This question is testing our ability to take derivatives of functions of multiple variables with respect to singular variablesFor example, w = xsin(y 3z) Partial derivatives are computed similarly to the two variable case For example, @w=@x means difierentiate with respect to x holding both y and z constant and so, for this example, @w=@x = sin(y 3z) Note that a function of three variables does not have a 9 Find ∂z ∂x ∂ z ∂ x and ∂z ∂y ∂ z ∂ y for the following function Okay, we are basically being asked to do implicit differentiation here and recall that we are assuming that z z is in fact z ( x, y) z ( x, y) when we do our derivative work Let's get ∂ z ∂ x ∂ z ∂ x first and that requires us to differentiate with




Derivative Of Log Y Mathematics Stack Exchange



Www Ucl Ac Uk Ucahjva Multi4 Pdf
Derivative of y = ln u (where u is a function of x) Unfortunately, we can only use the logarithm laws to help us in a limited number of logarithm differentiation question types Most often, we need to find the derivative of a logarithm of some function of xFor example, we may need to find the derivative of y = 2 ln (3x 2 − 1) We need the following formula to solve suchA partial derivative of a function is nothing but its derivative with respect to specific variables Since the question has not mentioned anything specific, I am just going to differentiate it with respect to mathx/math and mathy/math sepaSo in the last couple videos I talked about partial derivatives of multivariable functions and here I want to talk about second partial derivatives so I'm going to write some kind of multivariable function let's say it's I don't know sine of X times y squared sine of X multiplied by Y squared and if you take the partial derivative you have two options given that there's two variables you can



17 5 Higher Order Partial Derivatives Graphing Calculator By Mathlab User Manual




Finding The Derivative Of Log X Video Lesson Transcript Study Com
Draw graph Edit expression Direct link to this page Value at x= Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs ofBasic partial derivatives u = log( $x^2$ $y^2$ ), prove $ \frac{\partial^2 \;Calculus Find the Derivative d/dx y = log base 2 of x y = log2 (x) y = log 2 ( x) The derivative of log2(x) log 2 ( x) with respect to x x is 1 xln(2) 1 x ln ( 2)
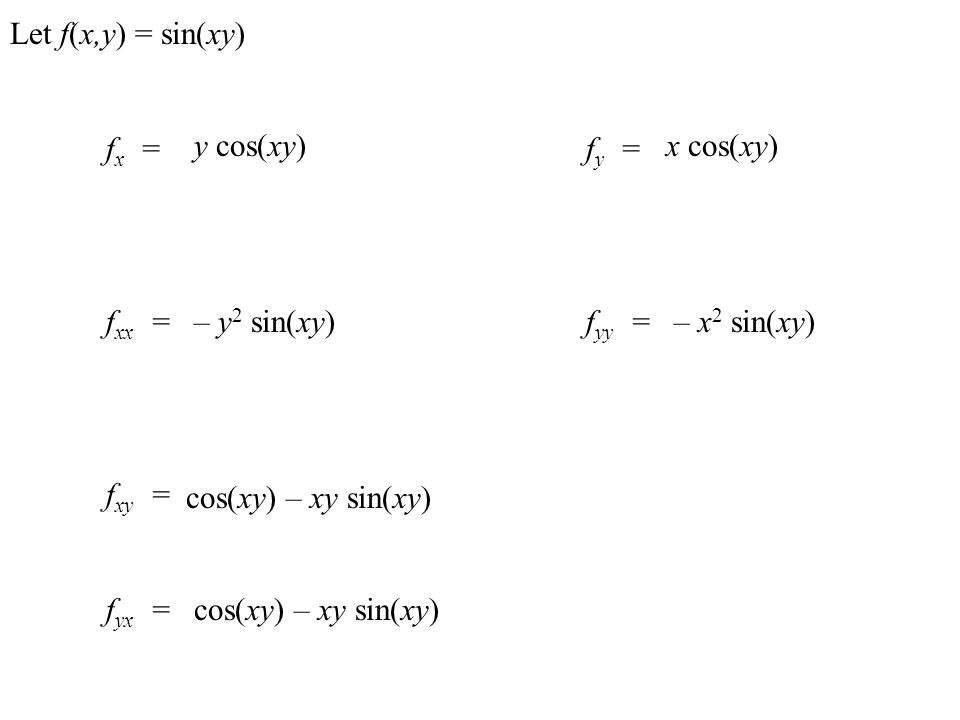



For Any Function F X Y The First Partial Derivatives Are Represented By F F Fx And Fy X Y For Example If F X Y Log X Sin Ppt Video
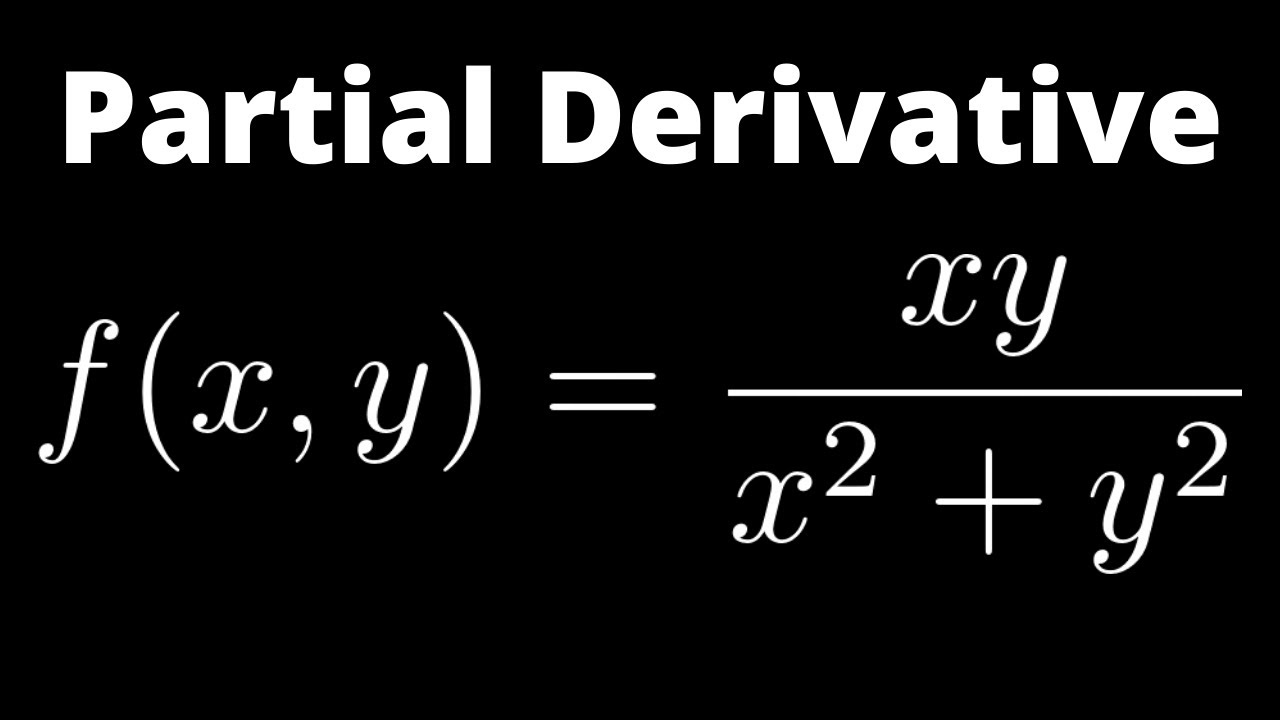



Partial Derivative Of F X Y Xy X 2 Y 2 With Quotient Rule Youtube
U}{\partial x \partial y} \; The partial derivative of f with respect to x is fx(x, y, z) = lim h → 0f(x h, y, z) − f(x, y, z) h Similar definitions hold for fy(x, y, z) and fz(x, y, z) By taking partial derivatives of partial derivatives, we can find second partial derivatives of f with respect to z then y, for instance, just as beforeApproximate partial derivatives from a table If the average value of f on the interval 2 to 4 is 3, then find the integral shown Find the partial derivatives of f (x,y,z)=xyz Find the partial derivatives of f (x,y,z)=xyz Find and interpret the partial derivatives of f (x,y)=3x2y4



5 Derivative Of The Logarithmic Function




Diploma Engineering Mathematics Notes
The estimate for the partial derivative corresponds to the slope of the secant line passing through the points (√5, 0, g(√5, 0)) and (2√2, 0, g(2√2, 0)) It represents an approximation to the slope of the tangent line to the surface through the point (√5, 0, g(√5, 0)), which is parallel to the x axis Exercise 1433@f @x = y3 2xy2;Constant, hence reappears in the derivative;



Http Www Math Ucsd Edu Benchow S10 e Derivative Pdf




If Y Log X Sqrt X 2 A 2 Show That X 2 A 2 D 2 Y Dx 2 X Dy Dx 0 Youtube
@f @y = x (d) f(x;y) = xe2x 3y;But in the 3x2y term 3x2 is a multiplicative constant, hence reappears in the derivative It multiplies the derivative of y, which is 1 (b) 2 1 z =(x2 y3)Derivatives of exponential and logarithmic functions d d x ( c a x ) = a c a x ln c , c > 0 {\displaystyle {\frac {d}{dx}}\left(c^{ax}\right)={ac^{ax}\ln c},\qquad c>0} the equation above is true for all c , but the derivative for c < 0 {\textstyle c




Chapter 5 Partial Differentiation Chapter 5 Partial Differentiation



12 3 Partial Derivatives Mathematics Libretexts
A brief overview of second partial derivative, the symmetry of mixed partial derivatives, and higher order partial derivativesמחשבונים לאלגברה, חשבון אינפיטיסימלי, גאומטריה, סטטיסטיקה, וכימיה כולל הדרךDerivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Functions Line Equations Functions Arithmetic & Comp Conic Sections Transformation




Unit Vi




Find All The First Order Partial Derivatives For The Chegg Com
There's a factor of 2 missing in all your second derivatives The result is exactly as you'd expect The variable you're differentiating with respect to, matters If it's x, then y is treated as a constant, and vice versa So if the "active" variable is leading in the numerator in one derivative, the same should apply in the otherAnswer to Find the partial derivative of the function z=x/x^2y^2 By signing up, you'll get thousands of stepbystep solutions to your homework@f @x = 3x2y ex;
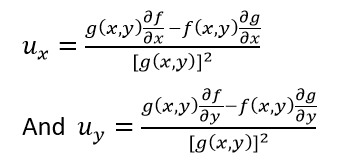



Partial Derivative Definition Formulas And Examples Partial Differentiation




Find The First Order Partial Derivatives Of The Chegg Com




Ex 5 7 9 Find Second Order Derivatives Of Log Log X




Derivative Of Log Log X 2 With Respect To X Is




Find The First Order Partial Derivatives Of The Fo Gauthmath




If U Log X 2 Y 2 Z 2 Then Prove That X 2 Y 2 Z 2 D 2u Dx 2 D 2u Dy 2 D 2u Dz 2 1
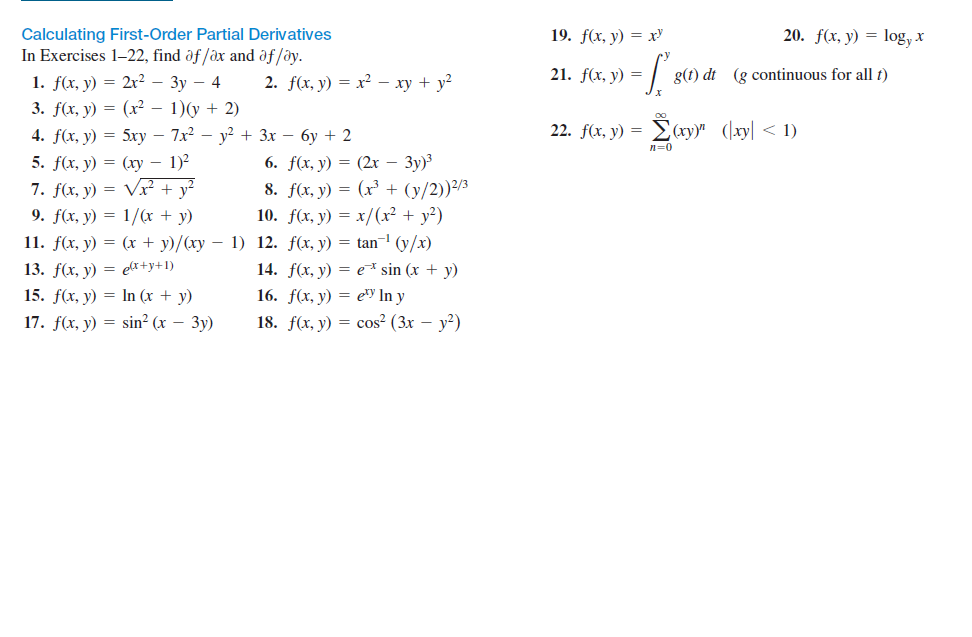



Answered Calculating First Order Partial Bartleby



What Is The Nth Derivative Of Logx Quora



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf



1




Partial Derivative Examples Math Insight




What Is The Second Derivative Of Y Log X 2 E X Quora
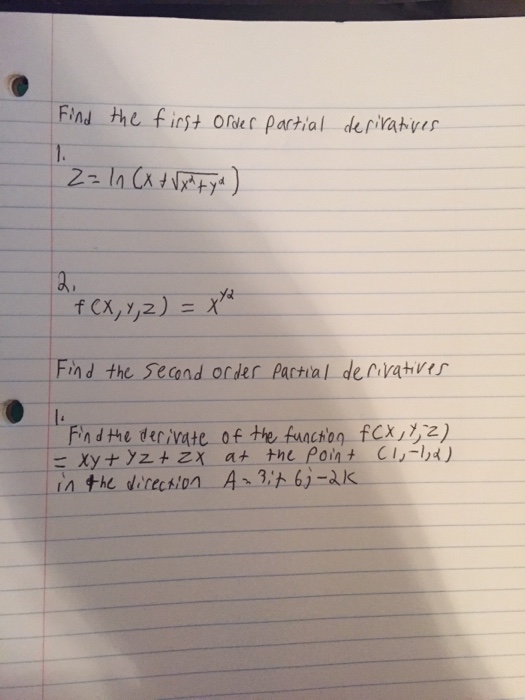



Find The First Order Partial Derivatives Z Ln X Chegg Com



5 Derivative Of The Logarithmic Function



What Is The Partial Derivative Of U Y X W R T To X And Y Quora




Natural Logarithm Wikipedia




Derivative Rules




Partial Derivative Examples Math Insight




Calculus 3 Partial Derivative 6 Of 30 Find The Partial Derivative Example 2 Youtube




Implicit Differentiation Advanced Example Video Khan Academy




If X Rcostheta Y Rsintheta Find Del X Y Del R Theta Del R Theta Del X Y
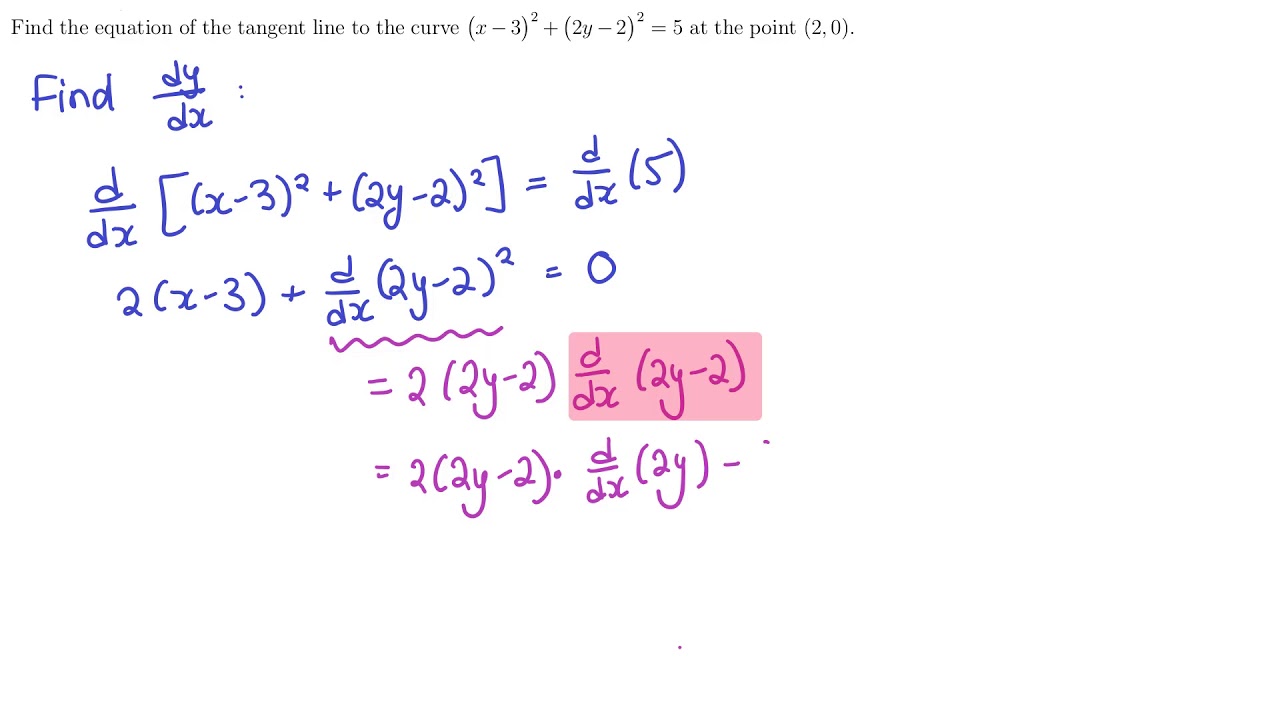



Implicit And Logarithmic Differentiation
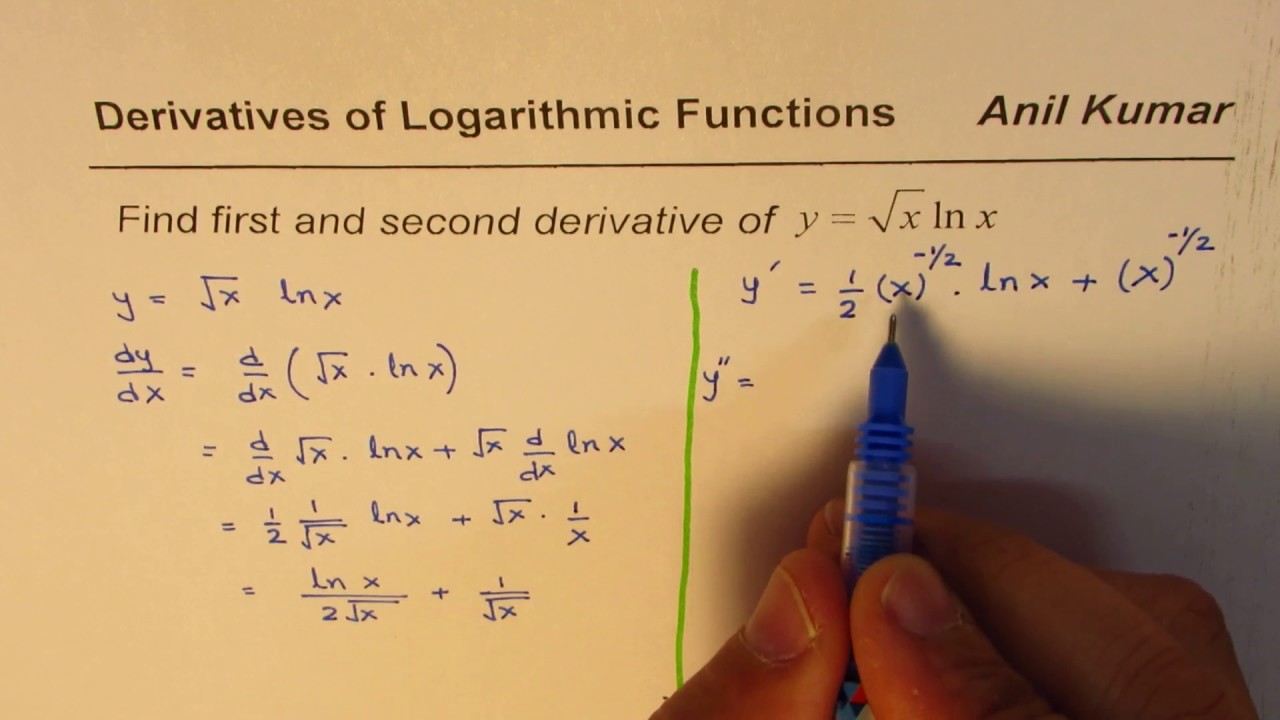



Find Second Derivative Of Log X Calculus Youtube




Derivative Of Log X Sqrt X 2 A 2 W R T X Is Youtube



Solved Form Partial Differential Equation By Eliminating The Arbitrary Function F Ax By Cz X 2 Y 2 Z 2 0 Also Find Order And Degree Of The Course Hero



Http Maths Dur Ac Uk Users Daniel Evans Mes Messolutionsupdated Pdf




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange




What Is The Partial Derivative Of Log With Respect To Y Homeworklib



5 Derivative Of The Logarithmic Function




4 2 Derivatives Of Logarithmic Functions




Derivative Calculator Wolfram Alpha




Find Nth Derivative Of Log X 2 A 2 Brainly In



Rules Of Calculus Multivariate



Q Tbn And9gcqnye10zfu7n1e5psc 7oyuuimkr8sjknkcqpbj1hdnr3gsgvai Usqp Cau



What Is The Derivative Of E Logx Quora




Rd Sharma Class 12 Maths Solutions Chapter 11 Differentiation




Doc Chapter Four Derivatives Of Multivariate Functions Partial Differentiation Habtamu Destaw Academia Edu



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf
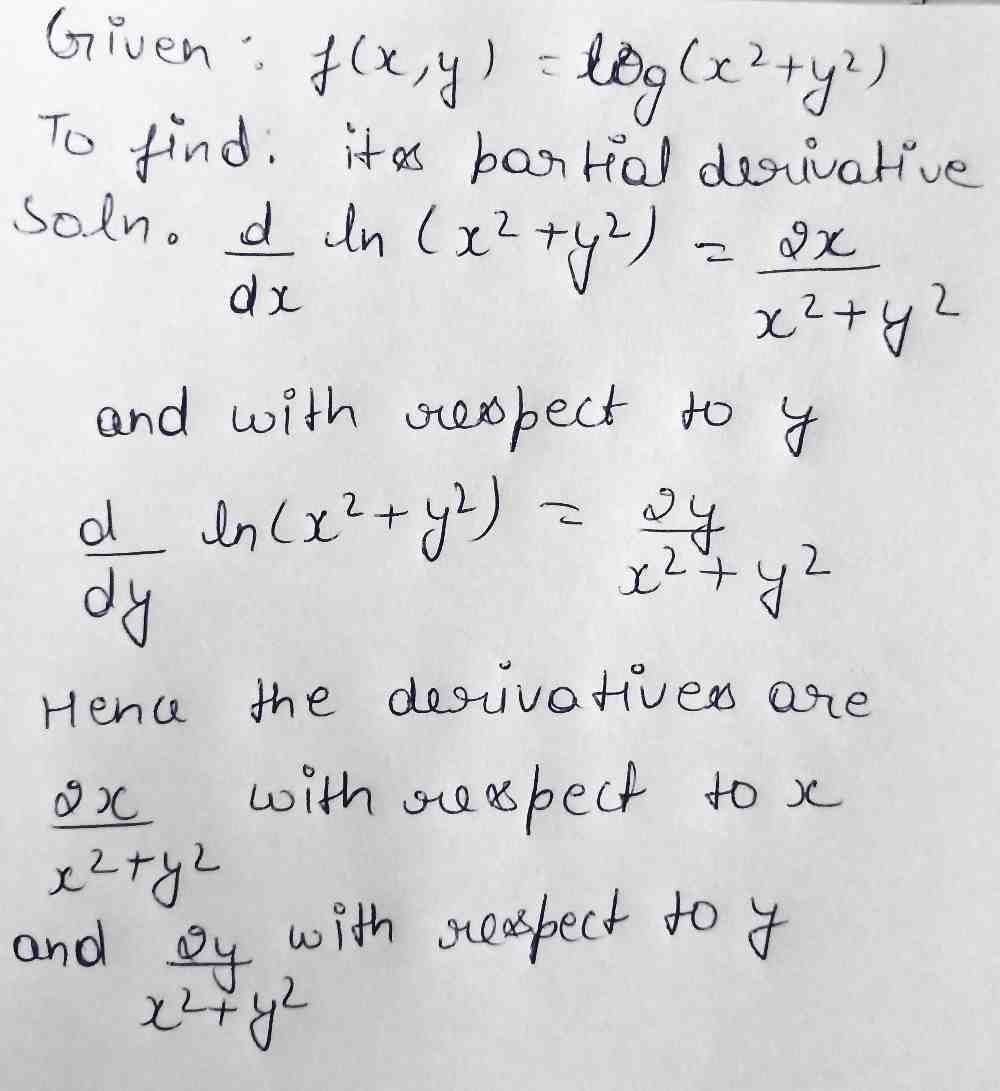



Partial Derivative Of Fx Y Ln X2 Y2 Gauthmath




Derivative Of Log Confusion Mathematics Stack Exchange
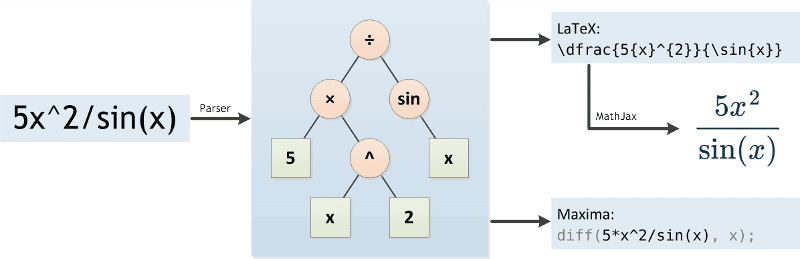



Derivative Calculator With Steps




Derivative Of X 2 Y 2 Log Xy Youtube
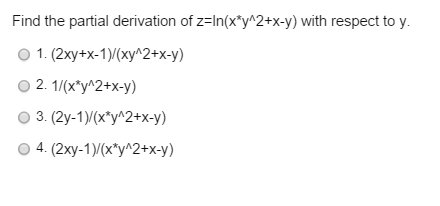



Find The Partial Derivative Of F X Y E X2 Y2 With Chegg Com




Derivative Of Logₐx For Any Positive Base A 1 Video Khan Academy




Solved 1 Use L Hopital S Rale To Derive The Following Li Chegg Com




What Is The Partial Derivative Of Cos Y X With Respect To X Quora



Finding The Derivative Of Log X Video Lesson Transcript Study Com




Finding The Derivative Of Log X Video Lesson Transcript Study Com



What Is The Nth Derivative Of Logx Quora




5 Derivative Of The Logarithmic Function
.gif)



Calculus Differentials And Integrals




Ex 5 7 10 Find Second Order Derivatives Of Sin Log X




If Logsqrt X 2 Y 2 Tan 1 Y X Then Dy Dx Is




Ex 5 7 9 Find Second Order Derivatives Of Log Log X




Partial Derivative Mcqs Assignement Maxima And Minima Rates



1




If U Log X 2 Y 2 Z 2 Verify 2u X Y 2u X Y




How To Calculate Fxy Partial Derivatives




First Order Partial Derivatives Of F X Y Ln X 4 Y 4 Youtube



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf



If X Y Y X What Is Dy Dx Quora




What Is The Derivative Of Log Y With Respect To X Mathematics Stack Exchange
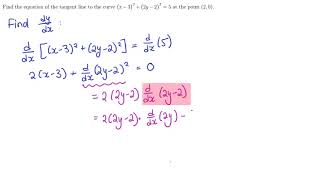



Implicit And Logarithmic Differentiation




Problems On Partial Differentiation U Log X 2 Y 2 Z 2 U Tan 1 2xy X 2 Y 2 Z F X Ay Q X Ay Youtube




Find All The Second Order Partial Derivatives Of The Chegg Com



Partial Derivatives



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau
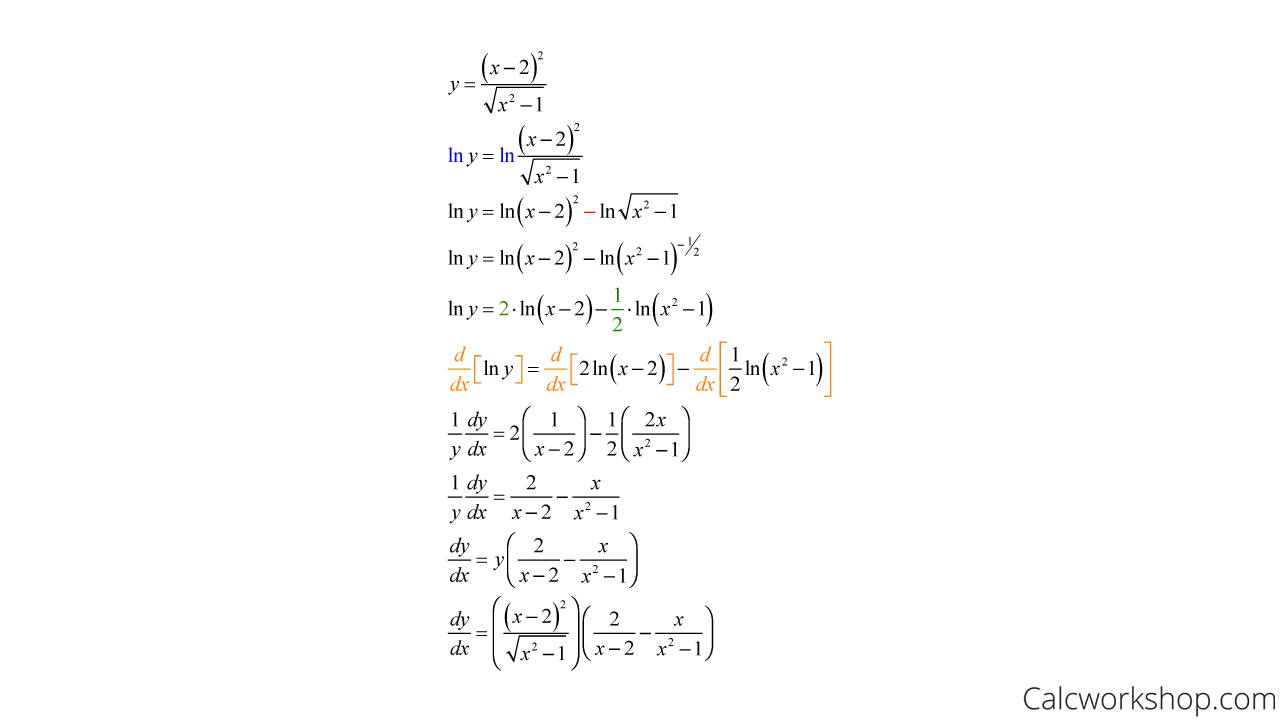



Logarithmic Differentiation W 7 Step By Step Examples




In Each Case Following Find The Partial Derivatives Chegg Com




1 Pages 1 33 Flip Pdf Download Fliphtml5



0 件のコメント:
コメントを投稿